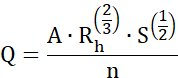Recibido: 21/06/2022, Aceptado: 30/07/2022 Artículo original
Métodos
numéricos aplicados al cálculo hidráulico en canales de regadío de Bagua
Numerical
methods applied to the hydraulic calculation of irrigation canals in Bagua
Métodos
numéricos aplicados para o cálculo hidráulico dos canais de irrigação em Bagua
Ronald Omar Estela Urbina1
*, Jhon
Jairo Danducho Paati1
Segundo
Marcial Chiclote Alcalde1, Fernando Alain Incio Flores1 Nemesio
Santamaría Baldera1, Roger Álvaro Fernández Villarroel1 Carlos
Carcausto Quispe2, Giovanna Guzmán Cáceres3 María
Elena Cárdenas León4, Daniel Jesús Castro Vargas4
RESUMEN
El
presente artículo evidencia la investigación realizada, ponderando la
importancia de la hidráulica en la formación académica del futuro ingeniero
civil, así mismo teniendo en cuenta la escasa infraestructura de riego en la
provincia de Bagua, que es eminentemente agrícola. El objetivo fue la revisión
de los factores hidráulicos de los distintos conductos abiertos existentes, ya
sean naturales o artificiales, así como la elaboración de modelos matemáticos
que permitan simular numéricamente el comportamiento hidráulico. Esta
investigación se realizó en el curso de Métodos Numéricos de la carrera de
Ingeniería Civil de la Universidad Nacional Intercultural “Fabiola Salazar
Leguía” de Bagua –UNIFSLB durante el año 2020 y 2021. La metodología consistió
en tres fases: La primera fase consistió en la obtención de datos en campo, en
la segunda fase se realizó cálculos informáticos utilizando el lenguaje de
programación Python, y en la última fase metodológica se procedió a elaborar e
implementar modelos o métodos matemáticos. Los resultados obtenidos para el
caudal y la velocidad difieren aproximadamente en 3% del valor teórico respecto
al valor medido en campo, de la misma forma se implementó programas para el
cálculo hidráulico. Finalmente se codificó los métodos numéricos para la
simulación numérica y gráfica.
Palabras claves: Método
numérico, canal hidráulico, Manning, Python.
ABSTRACT
This article evidences the research carried out,
considering the importance of hydraulics in the academic training of the future
civil engineer, also taking into account the scarce irrigation infrastructure
in the province of Bagua, which is eminently agricultural. The objective was
the review of the hydraulic factors of the different existing open conduits,
whether natural or artificial, as well as the elaboration of mathematical
models that allow numerically simulating the hydraulic behavior. This research
was carried out in the Numerical Methods course of the Civil Engineering career
of the National Intercultural University "Fabiola Salazar Leguía" of
Bagua -UNIFSLB during the year 2020 and 2021. The methodology consisted of
three phases: The first phase consisted of field data collection, in the second
phase computer calculations were performed using the Python programming
language, and in the last methodological phase we proceeded to develop and
implement models or mathematical methods. The results obtained for flow and
velocity differ by approximately 3% from the theoretical value with respect to
the value measured in the field, and programs for hydraulic calculation were
also implemented. Finally, the numerical methods for numerical and graphical
simulation were codified.
Keywords: Numerical method,
hydraulic channel, Manning, Python.
DOI: https://doi.org/10.55996/dekamuagropec.v3i1.70
1 Universidad Nacional Intercultural
Fabiola Salazar Leguía de Bagua. Perú, correo: restela@unibagua.edu.pe; jdanduchop@unibagua.edu.pe; schiclotea@unibagua.edu.pe; fincio@unibagua.edu.pe; nsantamaria@unibagua.edu.pe; rfernandez@unibagua.edu.pe
2Universidad Nacional del Altiplano.
Perú, correo: ccarcausto@unap.edu.pe
3Universidad Nacional San Antonio Abad
del Cuzco. Perú, correo: giovanna.guzman@unsaac.edu.pe
4Universidad Nacional Autónoma de Chota.
Perú, correo: mcardenas@unach.edu.pe; djcastrov@unach.edu.pe
RESUMO
Este artigo mostra a pesquisa realizada, considerando
a importância da hidráulica na formação acadêmica do futuro engenheiro civil,
bem como levando em conta a escassa infra-estrutura de irrigação na província
de Bagua, que é eminentemente agrícola. O objetivo era rever os fatores
hidráulicos dos diferentes condutos abertos existentes, sejam naturais ou
artificiais, bem como a elaboração de modelos matemáticos para simular
numericamente o comportamento hidráulico. Esta pesquisa foi realizada no curso
de Métodos Numéricos do curso de Engenharia Civil da Universidade Nacional
Intercultural "Fabiola Salazar Leguía" de Bagua -UNIFSLB durante os
anos de 2020 e 2021. A metodologia consistia em três fases: A primeira fase
consistiu na coleta de dados de campo, na segunda fase foram realizados
cálculos computadorizados utilizando a linguagem de programação Python, e na
última fase metodológica procedemos ao desenvolvimento e implementação de
modelos ou métodos matemáticos. Os resultados obtidos para o fluxo e velocidade
diferem em aproximadamente 3% do valor teórico em relação ao valor medido no
campo, e da mesma forma, foram implementados programas para o cálculo
hidráulico. Finalmente, os métodos numéricos para a simulação numérica e
gráfica foram codificados.
Palavras-chave: Método numérico, calha
hidráulica, Manning, Python.
INTRODUCCIÓN
La provincia de Bagua está rodeada de grandes
extensiones de tierras cultivables lo que hace imperiosa la necesidad de un
buen manejo del recurso hídrico, no solo en su uso, sino también a su
conducción. Los ríos que recorren la región de Amazonas y todo el nor-oriente
del territorio peruano alimentan a toda una red de derivaciones o canales
emergentes (Hernández, Rivas, & Feliu, 2020), cuya labor de la ingeniería
es conducir con la mayor de las eficiencias a las parcelas agrícolas (Gonzáles,
2020).
Los canales de regadío que se encuentran en esta
zona tropical del Perú, son naturales y artificiales, existiendo en esta región
actualmente gran demanda de infraestructura hidráulica de eficiencia (Alfaro,
Guerra, & Olivares, 2020). El diseño de estructuras de conducción de fluido
por gravedad implica una revisión de parámetros físicos y geométricos de los
canales ya existentes y proponer mejoras, lo cual hace imperiosa la necesidad
de un modelamiento numérico (J. Hernández & Martínez, 2019).
En condiciones hidráulicas de flujo uniforme es
decir que: tirante hidráulico, velocidad, área, caudal entre otros parámetros
no varían con respecto al espacio, es decir se mantienen constantes, de
cumplirse esta condición, dicho flujo permanente recibe el nombre de flujo
normal (Pantaleón et al., 2019). La expresión empírica más usada y que reúne
parámetros físico geométricos es la fórmula de Manning:
Donde V representa la velocidad del
fluido, Rh es el radio hidráulico, S pendiente del canal, n es el coeficiente
de rugosidad.
Haciendo uso del principio de
continuidad podríamos definir el caudal (Q) que trastada una determinada
sección hidráulica (A):
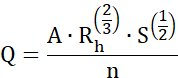
El volumen de agua que transporta una
determinada sección transversal en el tiempo se le denomina caudal como podemos
apreciar en la expresión anterior, de la cual se deduce que no solo depende de
la máxima sección hidráulica, sino también de las condiciones de revestimiento
y conservación de la infraestructura, esto es de la rugosidad que presente el
perímetro mojado del canal (Asalde, 2020).
En el análisis hidráulico de los canales de regadío
de Bagua se debe tener en cuenta los elementos geométricos de los mismos (Fatehi,
Hajikandi, Hassanzadeh, & Jamali, 2019), así como la disponibilidad del
terreno y volumen de transporte del recurso hídrico. Los canales artificiales
generalmente se diseñan con formas geométricas regulares (tabla 1), siendo la
región trapezoidal la que transporta mayor volumen de fluido (Gutierrez, 2020).
Tabla 1. Análisis
geométrico de los canales de regadío de Bagua capital
Otro principio fundamental en la hidráulica es la conservación
de la energía, que da origen a la ecuación de Bernoulli, de donde se define la
energía por kilogramo de agua que fluye a través de la sección transversal
referenciada respecto al fondo del canal (Deza & Castañeda, 2020), esta se
denomina Energía específica (E). Este concepto fue utilizado primigeniamente en
el año 1912 por Boris A. Bakhmetteff, siendo esta una adecuada estrategia para
resolver situaciones problemáticas de complejas transiciones cortas teniendo en
cuenta que las pérdidas por fricción o rozamiento resultan despreciables
(Cadena, Saltos, & Villalta, 2018).
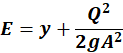
Un “indicador” que nos permitirá caracterizar el
flujo de superficie libre, es el número de Froude (F) este es una constante
adimensional que refleja la relevancia de las fuerzas inerciales y
gravitacionales (Sánchez, Gómez, & Bladé, 2020). Donde:
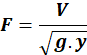
En la Tabla 2, se muestra los tipos de flujo en un canal
considerando la fórmula del número de Froude (F).
Considerando la importancia de la
temática desarrollada anteriormente y teniendo en cuenta la escasa
infraestructura hidráulica en la provincia de Bagua, el objetivo de este trabajo
de investigación fue la revisión de los factores hidráulicos de los distintos
conductos abiertos existentes, ya sean naturales o artificiales, así como la
elaboración de modelos matemáticos que permitan simular numéricamente el
comportamiento hidráulico, y que de esta manera sirva como insumo para futuros
proyectos de implementación en la zona norte de la región Amazonas-Perú.
MATERIALES Y MÉTODOS
Esta investigación se realizó en el curso de Métodos
Numéricos de la carrera de Ingeniería Civil de la Universidad Nacional
Intercultural “Fabiola Salazar Leguía” de Bagua –UNIFSLB durante el año 2020 y
2021. Se considero tres fases: La primera fase consistió en la obtención de
datos en campo, por medio de mediciones directas e indirectas en los canales de
Bagua (Cadena et al., 2018), con respecto a la información recolectada se
utilizó el software de información geográfica, en este caso Google Earth (J.
Hernández & Martínez, 2019). Los datos obtenidos se organizaron en tablas
donde incluía los factores geométricos como tirantes agua, ancho de solera,
talud y pendiente del canal, así mismo se aplicó principios físicos para
determinar el caudal del canal aplicando el principio de continuidad (Cadena et
al., 2018). Como segunda fase se realizó cálculos informáticos utilizando el
lenguaje de programación Python, donde aplicando la fórmula de Manning permitió
corroborar y discriminar los datos obtenidos y de esta manera hacer una
revisión de los factores hidráulicos de los canales, como última fase
metodológica se procedió a elaborar e implementar modelos o métodos matemáticos
que permitan la simulación numérica y de esta forma obtener las condiciones
óptimas para el funcionamiento hidráulico del canal (Ladino, García &
García, 2020b).
Los métodos o modelos matemáticos utilizados en esta
investigación están referidos al cálculo de raíces de una ecuación,
diferenciación e integración numérica, así como interpolación.
Cálculo de raíces: Newton-Raphson
Dada la función diferenciable f: R→R y una
aproximación inicial x_0 para obtener la solución a f(x)=0 la iteración del
método de Newton está por:
Donde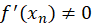 
para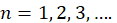 
.
Cálculo de raíces: Interacción de Punto fijo
Establece que:
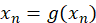
para .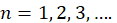
En este estudio se aplicó los métodos directos,
donde el caudal del canal se determinó resolviendo la ecuación de Manning (Terán
& Rúa, 2018).
Integración numérica: Regla de
Simpson
Los métodos numéricos existentes para estimar el área
debajo de una curva son variados, sin embargo, los más usuales y elementales
como el trapezoidal y rectangular generan márgenes de error considerables, por
lo tanto, planteamos como algoritmo la Regla de Simpson (Figura 1), cuya
segmentación de la figura no es lineal, lo que permite un mejor ajuste y cercanía
a la figura original (Peña & Rivas, 2019).
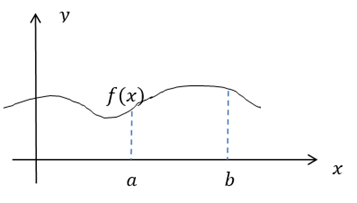
Figura 1. Integración numérica: Regla de
Simpson
Para esta regla dividiremos el intervalo [a,b] en 
subintervalos de longitud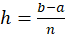 
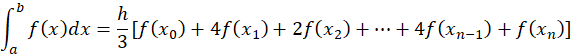
Siendo este el valor de la integral donde el valor de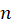 
sea siempre un número par.
Interpolación numérica: Polinomio de
Lagrange
En algunos casos no se dispone de una
ecuación o función que permita la manipulación de las variables para su
respectivo cálculo, todo lo contrario, se cuenta con pares ordenados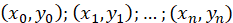 
El polinomio de Lagrange se expresa(Carnero, 2018):
Diferenciación numérica
En hidráulica, una de las mediciones directas que
podemos realizar es el volumen hídrico por de una determinada sección
transversal, tomando como referencia el tiempo, ambas magnitudes físicas que se
relacionan con el caudal, teniendo en cuenta que este es la razón temporal de
cambio del voumen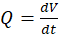 
(Duran, Páez, & García, 2018).
Si conocemos los puntos 
, los cuales se hallan equi espaciados:
.
.
.
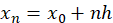
Para el primer intervalo [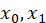
], se evalúo numéricamente la primera derivada de la
función 
en el punto medio del intervalo asumido: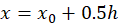 
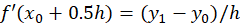
En esta primera fase, se muestra el caudal que
transportan los canales de regadío en Bagua suelen ser variables durante el
año, conocedores de ello se registró mediciones en los meses de diciembre
(2020), abril y mayo del presente año 2021, donde se obtuvo la ubicación,
clasificación y toma de datos de los factores hidráulicos de los canales
abiertos (Figura 2).
Figura 2. Realizando mediciones en
canales de Bagua - La Peca
En la tabla 3, se observa la
clasificación y medición de los canales de regadío de Bagua, para los meses de
evaluación (primera semana de diciembre 2020, tercera semana de abril 2021, segunda
semana de mayo 2021).
Tabla 3. Ubicación, clasificación y medición de factores
hidráulicos en canales de regadío de Bagua-Amazonas
|
Forma del canal y ubicación
|
Ancho de solera(b) en metros
|
Espejo de agua(T) en metros
|
Talud(Z)
|
Pendiente(S)
|
Tirante de agua(y) en metros
|
Material de construcción de canal(n)
|
|
Rectangular(Achaguay bajo)***
|
0.95
|
0.95
|
0
|
0.0048
|
0.23
|
0.014
|
|
Rectangular(Achaguay bajo)**
|
0.95
|
0.95
|
0
|
0.0045
|
0.03
|
0.014
|
|
Rectangular(Achaguay bajo)*
|
0.95
|
0.95
|
0
|
0.0056
|
0.1352
|
0.014
|
|
Parabólico de tierra(Peca Palacios)**
|
0
|
2.08
|
0
|
0.0123
|
0.261
|
0.050
|
|
Parabólico de tierra(Peca Palacios)**
|
0
|
3.62
|
0
|
0.0084
|
0.18
|
0.050
|
|
Trapezoidal(Amoja-Aramango)***
|
1.62
|
2.47
|
1.88
|
0.0032
|
0.80
|
0.015
|
|
Trapezoidal (San Francisco)**
|
0.39
|
0.69
|
1.6
|
0.0024
|
0.24
|
0.013
|
|
Trapezoidal(San Francisco)*
|
0.382
|
0.56
|
0.75
|
0.02619
|
0.12
|
0.015
|
|
Trapezoidal(La Peca)**
|
0.5
|
1.6
|
0.37
|
0.0005
|
0.2
|
0.014
|
|
Rectangular(La Peca)**
|
0.65
|
0.065
|
0
|
0.0008
|
0.5
|
0.014
|
|
Rectangular(La puntilla – Valencia)**
|
0.90
|
0.90
|
0
|
0.005
|
0.06
|
0.013
|
|
Trapezoidal (La Peca)***
|
0.40
|
0.94
|
1.48
|
0.087
|
0.40
|
0.013
|
|
Rectangular(La Peca)*
|
0.80
|
0.80
|
0
|
0.087
|
0.662
|
0.013
|
|
Rectangular (San Francisco)**
|
0.61
|
0.61
|
0
|
0.0026
|
0.23
|
0.014
|
|
Rectangular(Toma comunal de Bagua)
|
0.95
|
0.95
|
0
|
0.0067
|
0.17
|
0.013
|
|
Rectangular(La puntilla)***
|
0.94
|
0.94
|
0
|
0.005
|
0.168
|
0.013
|
*primera semana de diciembre
2020; **tercera semana de abril 2021; ***segunda semana de mayo 2021
Factores hidráulicos como espejo de agua(T), tirante
de agua(y), ancho de solera(b), Talud(Z) o pendiente(S) se obtenidas mediante
mediciones directas, haciendo uso de instrumentos de medición de longitud como
cintas métricas, cuya resolución o lectura mínima es el milímetro (0.001 m),
así también niveles de burbuja (Figura 3).
Figura 3. Determinación de la pendiente (A); Aforo de un
canal (B)
Con respecto a magnitudes
físicas – hidráulicas inherentes al escurrimiento de un fluido, tal como
volumen o caudal en un canal abierto, es necesario medir el aforo para lo cual
en esta investigación optamos por el método del flotador. En la tabla 4, se
puede visualizar las variables físicas e hidráulicas encontradas.
Tabla 4. Variables físicas-hidráulicas obtenidas por el
método del flotador y Ecuación de continuidad
|
Forma del canal
|
Longitud del tramo(L)
en metros
|
Tiempo promedio(t) en segundos
|
Estimación del área hidráulica(A) en
metros cuadrados
|
Velocidad del fluido(v) en mestros por
segundo
|
Estimación del caudal(Q) en metros
cúbicos por segundo
|
|
Parabólico de tierra(Peca Palacios)*
|
10.00
|
19.800
|
|
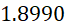
0.52
|
|
|
Rectangular(La Peca)*
|
10.00
|
14.130
|
0.3250
|
0.7077
|
0.2300
|
|
Trapezoidal(La Peca)*
|
7.00
|
6.3915
|
0.2100
|
1.0952
|
0.2300
|
|
Rectangular(Achaguay bajo)***
|
8.00
|
7.2900
|
0.2185
|
1.0970
|
0.2808
|
|
Rectangular(Achaguay bajo)**
|
5.00
|
10.760
|
0.1254
|
0.4647
|
0.0597
|
|
Rectangular(Achaguay bajo)*
|
9.10
|
7.8790
|
0.1284
|
1.1549
|
0.1483
|
|
Parabólico de tierra( Peca Palacios)*
|
15.00
|
21.440
|
3.2151
|
0.6996
|
2.2527
|
|
Rectangular (San Francisco)***
|
4.40
|
6.2520
|
0.1403
|
0.7038
|
0.0987
|
|
Trapezoidal (San Francisco)***
|
5.00
|
6.3080
|
0.2220
|
0.7926
|
0.1760
|
|
Rectangular(Toma comunal de Bagua)**
|
9.00
|
8.2800
|
0.1650
|
1.0869
|
0.1793
|
|
Rectangular(La puntilla)***
|
6.00
|
4.1250
|
0.1579
|
|
|
|
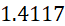
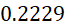
Trapezoidal(Amojao-Aramango)***
|
12.00
|
9.7400
|
1.6360
|
1.2320
|
2.0156
|
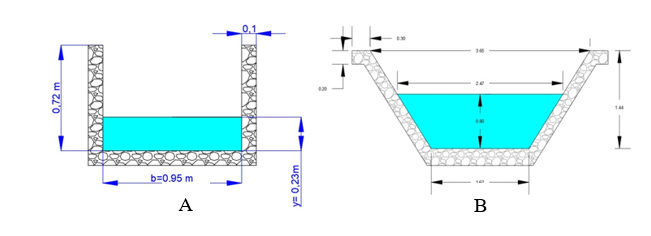
Figura 4, se muestra las secciones
transversales en canales artificiales (diseñado en AutoCAD), los canales de
regadío de Bagua resultan ser rectangular y trapezoidal. Así mimo en la figura 5,
se muestra las imágenes reales de los canales.
Figura 4. Sección transversal:
rectangular del canal Toma Municipal (A) – trapezoidal canal del Amojao – Bagua
(B).
Figura 5. Tipos de canales para regadío en Bagua capital
La segunda fase corresponde a
la codificación de los programas. Como se desarrolló anteriormente, la fórmula
de Manning es una expresión matemática empírica que permite determinar el caudal
de un canal abierto, del cual se dispone o se conoce los elementos geométricos
de la estructura hidráulica. Ya que estos procesos matemáticos son complicados
y requieren muchas interacciones para la búsqueda de soluciones, se realizaron
programas en Python, así mismo se codificaron los cálculos correspondientes a
la energía mínima y su relación con el caudal (Figura 6).
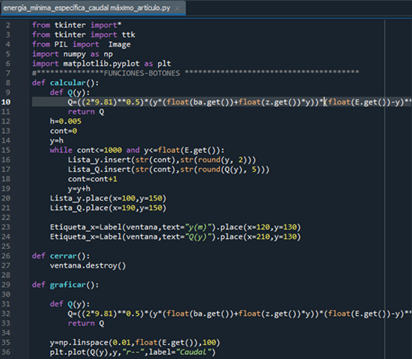 Figura 6. Código fuente en Python
|
|
Figura 7, se muestra los resultados entre el caudal y el
tirante, lo cual es el reflejo de ciudad de Bagua.
Figura 7. Interfaz gráfica del ingreso de elementos
geométricos del canal (A); Relación entre el caudal y el tirante (B)
En la tercera fase se muestra las condiciones
hidráulicas de los canales de Bagua, donde se procedió a elaborar modelos o
métodos numéricos que permita en algunos casos validar las medidas obtenidas
por los estudiantes y en otros casos explicar el comportamiento hidráulico
simulando diversos valores de variables (Figura 8).
Figura 8. Interfaz gráfica del ingreso del volumen del canal
y la variación temporal del volumen del canal
En la figura 9, se muestra los
valores encontrados para los canales de Bagua, donde la pendiente en campo fue
de 0.00335, la velocidad superficial del fluido fue 1.097 m/s.
Figura 9. valores encontrados para los canales de Bagua
Luego se calculó los porcentajes de error de la
velocidad tanto obtenidos en campo y los valores teóricos aplicando la ecuación
de Manning (Figura 10).
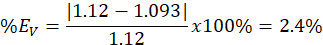
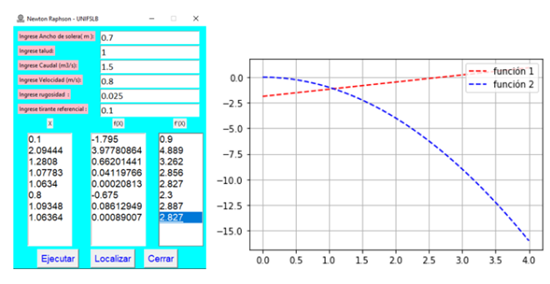
Figura 10. Solución numérica para
el tirante de un canal trapezoidal
Una de las fortalezas del
lenguaje Python fue la realización de gráficos con mucha facilidad, así como el
ingreso y manejo de funciones, lo que permitió codificar los métodos numéricos
y la búsqueda de raíces de forma gráfica.
def ejecutar():
def f(x):
f=float(ba.get())*x-float(Q.get())/float(V.get())+float(z.get())*x**2
return f
def d(x):
d=float(ba.get())+2*float(z.get())*x
return d
y=float(yp.get())
print (y)
cont=0
x_x=y
while
abs(f(x_x))>0.00001:
Lista_x.insert(str(cont),str(round(x_x, 5)))
Lista_fx.insert(str(cont),str(round(f(x_x), 8)))
Lista_dx.insert(str(cont),str(round(d(x_x), 3)))
cont=cont+1
x_x=x_x-f(x_x)/d(x_x)
Lista_x.place(x=30,y=220)
Lista_fx.place(x=160,y=220)
Lista_dx.place(x=300,y=220)
Figura 11, se muestra la
interfaz gráfica para los ingresos de los elementos geométricos del canal y las
curvas de energía especifica.
Figura 11. Solución numérica y gráfica para el tirante
crítico para un determinado caudal evaluando su energía específica.
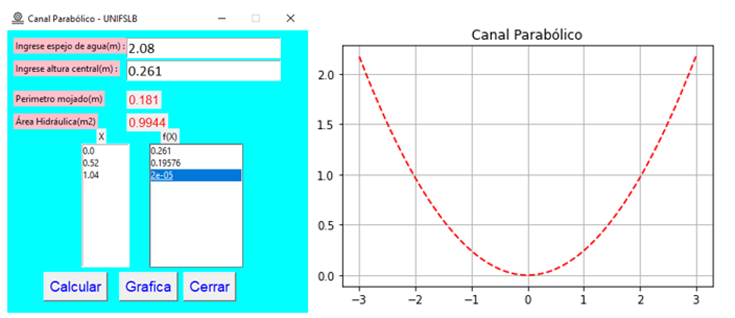
Figura 12, se muestra los
resultados de canales naturales o de tierra existentes en la provincia de Bagua
podríamos aproximarlo a una sección parabólica, lo cual en esas condiciones
tanto el perímetro mojado como el área hidráulica resulta producto de la
evaluación de la integral de la función cuadrática, que es la que más describe
su geometría del canal.
Figura 12. Integración numérica para determinar el perímetro
mojado y el área hidráulica en un canal parabólico
DISCUSIÓN
El uso de un lenguaje de programación como el Python en la enseñanza
del curso de métodos numéricos resultó una oportunidad propicia para traducir
todos los fenómenos físico- hidráulicos en ecuaciones calculables (Lima,
Cedeño, & Padilla, 2020), y de esta forma manipular variables y generar
nuevos resultados de forma gráfica y numérica, lo cual le sirve para su formación
profesional, y en un futuro muy cercano en su quehacer profesional de la
ingeniería en la región de Amazonas y todo el Perú (Fernández de Córdova, León,
Rodríguez, Martínez, & Meneses, 2018).
En la selección de los métodos numéricos referidos al cálculo de raíces
(Sablón & De Arma, 2019), empleados en la presente investigación se tuvo en
cuenta métodos en los cuales se requiere no un intervalo, sino más bien un
punto inicial, y a partir de ello, comenzar las interacciones, sin embargo, se
sugiere hacer un análisis más profundo respecto a la eficiencia y manejo de
error haciendo una comparación entre métodos. Se debe advertir que, en muchos
de los libros de hidráulica, los autores sugieren localizar raíces de la
ecuación por el método de “tanteo”, lo cual quita rigor matemático al proceso (Pineda
& Chica, 2020).
Es necesario poner en evidencia que el estudio se realizó en una zona
tropical como es la zona nororiental del Perú. Este detalle resulta importante
hacerlo notar, ya que permite afinar el análisis respecto al comportamiento de
la viscosidad del agua, ya que la mayoría de tablas que referencian los libros
de hidráulica trabajan con valores referenciales de temperatura ambiente de
otras latitudes (Caparicona, 2020).
El uso del cálculo automatizado o por medio del ordenador, despertó el
interés de los estudiantes de ingeniería (Arévalo & González, 2020). La
creación de sus propias aplicaciones o pequeños programas para abreviar los
procesos operativos, dejaron en evidencia que el uso de un lenguaje de programación
es una estrategia efectiva para generar en los estudiantes aprendizajes
significativos y motivación permanente (Segarra, 2020).
Las obras hidráulicas existentes en Bagua son producto de diseño y
cálculo, que a la luz de la teoría deben ser corroboradas, lo que representa
una estrategia motivadora para los estudiantes, toda vez que encuentran más
vivencial esta actividad a través de un curso que por naturaleza resulta ligado
al formalismo abstracto, pese a ello los estudiantes de ingeniería civil de la UNIFSLB
realizaron la labor de recolección de datos como parte del desarrollo del curso
de métodos numéricos (Arévalo & González, 2020). Los algoritmos
desarrollados en el presente trabajo fueron codificados en lenguaje de
programación Python. La primera labor de los estudiantes fue solucionar por
medio de nuestras aplicaciones los ejercicios propuestos en los libros de
Hidráulica de canales con la finalidad de depurar la mayor cantidad de errores,
y de esa forma afinar detalles para la versión definitiva, luego aplicarla a
realidades de canales de Bagua (Ladino, García, & García, 2020a).
CONCLUSIONES
Se clasificó los canales según su sección transversal y se recolectó
datos de variables hidráulicas de los diferentes conductos abiertos para regadío
en Bagua.
Se elaboró algoritmos e implementó los métodos numéricos en el
lenguaje de programación Python para el cálculo hidráulico, así como la
estimación de variables en diferentes condiciones.
Se comparó los valores obtenidos en campo de velocidad y caudal con las
ecuaciones teóricas de Manning llegando a demostrar que la velocidad presenta
un error relativo por debajo del 3% aproximadamente.
Se obtuvo soluciones numéricas y graficas del
comportamiento hidráulico del canal a distintos valores de caudal, así mismo se
solucionaron las ecuaciones de Manning para caudal y velocidad.
REFERENCIAS BIBLIOGRÁFICAS
Alfaro, M., Guerra, R., & Olivares, A. (2020).
Evaluación de la profundidad de recursión de la solución analítica de la
ecuación de Colebrook-White en la exactitud de la predicción del factor de
fricción. Ingeniería, Investigación y Tecnología, 21(4), 1–15.
https://doi.org/10.22201/fi.25940732e.2020.21.4.036
Aponte, C. (2019). Diseño y construcción de una
canaleta Parshall para el Laboratorio de Hidráulica de la Universidad Santo
Tómas (UNIVERSIDAD SANTO TOMÁS). Retrieved
from
https://repository.usta.edu.co/bitstream/handle/11634/30431/2020carlosaponte.pdf?sequence=6
Arévalo, B., & González, A. (2020). Enseñanza de
integrales mediante métodos numéricos pormedio del uso de las TIC. Sinergias Educativas, 5(4), 21–34.
Retrieved from
http://sinergiaseducativas.mx/index.php/revista/article/view/155/442
Asalde, J. (2020). Diseño del canal de riego con
máxima eficiencia hidráulica mediante el software Hec-Ras, en el distrito de
Salas
(Universidad San Martín de Porres). Retrieved from
https://hdl.handle.net/20.500.12727/6942
Cadena, C., Saltos, M., & Villalta, M. (2018). Comparación
de tipos de flujos, para diferentes secciones de canales. (Escuela Superior
Politécnica del Litoral). Retrieved from
https://www.researchgate.net/publication/322555700_Comparacion_de_tipos_de_flujos_para_diferentes_secciones_de_canales
Caparicona, J. (2020). Elaboración de un programa
informático de aplicación para diseño agronómico e hidráulico en el método de
riego por goteo. Revista
Apthapi, 6(2), 1935–1953. Retrieved from
http://ojs.agro.umsa.bo/index.php/ATP/article/view/410
Carnero, E. (2018). Análisis numérico de infiltración
de agua en un suelo residual no saturado utilizando la curva de retención de
agua. Revista de Investigaciones Altoandinas, 20(4), 439–450. Retrieved from
http://www.scielo.org.pe/scielo.php?script=sci_arttext&pid=S2313-29572018000400007
Deza, J., & Castañeda, H. (2020). Hierofonía y
matemática del canal Cumbemayo. Cajamarca. Perú. Revista Ciencia y Desarrollo,
23(4), 67–102. https://doi.org/http://revistas.uap.edu.pe/ojs/index.php/CYD/index
Duran, M., Páez, J., & García, P. (2018). Modelado
numérico y análisis experimental para flujos en un medio poroso homogéneo a
través de suelos. Iteckne,
15(1), 24. https://doi.org/10.15332/iteckne.v15i1.1961
Fatehi, B., Hajikandi, H., Hassanzadeh, Y., &
Jamali, S. (2019). Investigación
experimental y analítica de los efectos de las células secundarias actuales en
las características del salto hidráulico en canales trapezoidales. Tecnologia y
Ciencias Del Agua, 10(3), 190–218. https://doi.org/10.24850/j-tyca-2019-03-08
Fernández de Córdova, C., León, A., Rodríguez, Y.,
Martínez, P., & Meneses, D. (2018). Influencia del método de estimación en
el coeficiente de Manning para cauces naturales. Ingeniería Hidráulica y
Ambiental, 39(1), 17–31.
Gonzáles, D. (2020). Modelo hidráulico virreinal
utilizado en el centro histórico de Lima para abstecimiento de agua. Devenir,
7(14), 91–106. https://doi.org/https://doi.org/10.21754/devenir.v7i14.811
Gutierrez, E. (2020). Consideraciones mínimas para el
diseño hidráulico de proyectos de infraestructura menor en canales abiertos
(Universidad Peruana Unión). Retrieved
from https://drive.google.com/file/d/1_lR8G2xOKhcG-2YVMyc1XXEeJ99GQQ2s/view
Hernández, J., & Martínez, S. (2019). Tránsito de
avenidas en vasos: ¿hidrológico o hidráulico? Tecnologia y Ciencias Del Agua,
10(6), 147–177. https://doi.org/10.24850/j-tyca-2019-06-06
Hernández, Y., Rivas, R., & Feliu, V. (2020).
Control automático de la distribución de agua en sistemas de riego: revisión y
retos. Revista Ingeniería Electrónica, Automática y Comunicaciones I, 41(2),
80–97. Retrieved
Ladino, E., García, C., & García, M. (2020a).
Flujo crítico en canales abiertos, solución numérica mediante el método de
Newton-Raphson para aplicación Android 4.0. Tecnura, 24(63), 99–114.
https://doi.org/10.14483/22487638.16196
Ladino, E., García, C., & García, M. (2020b). LA
IMPLICANCIA ECONÓMICA MEDIANTE NEWTON RAPSHON PARA EL DESARROLLO DE UNA
APLICACIÓN ANDROID PARA EL DISEÑO DEL DIÁMETRO DE TUBERÍAS A PRESIÓN. Aglala, 11(1), 29–50. Retrieved from
http://revistas.curnvirtual.edu.co/index.php/aglala/article/view/1577
Lima, R., Cedeño, J., & Padilla, M. (2020).
Aplicación de los métodos numéricos en la enseñanza superior. Revista Sinapsis,
1(16), 1–7. Retrieved from https://www.itsup.edu.ec/sinapsis
Pantaleón, J., Pérez, P., Cordero, R., Torres, A.,
García, B., Castillo, H., … Rivas, G. (2019). Determinación del coeficiente de
rugosidad para encachado usado en el revestimiento de cunetas en la República
Dominicana. Ciencia y Sociedad, 38(3), 551–568.
Peña, C., Ramirez, M., & Rivas, E. (2019). La
integración numérica en la integral definida : caso de estudio. Revista
Espacios, 40(19), 23.
Pineda, J., & Chica, E. (2020). Métodos numéricos
para el desarrollo de una turbina hidrocinética tipo Gorlov. Revista UIS
Ingenierías, 19(3), 187–205. https://doi.org/10.18273/revuin.v19n3-2020018
Sablón, L., & De Arma, A. (2019). Implementación
de métodos numéricos para resolución de sistemas de ecuaciones no lineales.
Ciencia & Futuro, 9(1), 74–100. Retrieved from http://revista.ismm.edu.cu/index.php/revista_estudiantil/article/view/1772
Sánchez, E., Gómez, M., & Bladé, E. (2020).
Análisis numérico 3D de las características del flujo en un canal curvo.
Ingeniería Del Agua, 24(3), 157–169. https://doi.org/10.4995/ia.2020.12276
Segarra, J. (2020). Análisis De Los Métodos Numéricos
En Ecuaciones Diferenciales Ordinarias Utilizando Mathematica. Revista
Ingeniería, Matemáticas y Ciencias de La Información, 7(13), 13–23.
https://doi.org/10.21017/rimci.2020.v7.n13.a72
Terán, J., & Rúa, C. (2018). El método de Newton
para raices complejas. Revista EIA, 15(29), 97–108. https://doi.org/https://doi.org/10.24050/reia.v15i29.1131
