Recibido: 18/11/2021, Aceptado: 19/02/2021
Artículo original
Etnomatemática:
Hidráulica lúdica a partir de las figuras geométricas de la cerámica awajún
Ethnomathematics:
Playful hydraulics from the geometric figures of awajún ceramics
Etnomatemática: a hidráulica
lúdica a partir das figuras geométricas da cerâmica Awajún
Ronald Omar Estela Urbina1 *, Elisa
Contreras Barsallo2
*, Elisa
Contreras Barsallo2 Jean
Erich Vásquez Delgado3
Jean
Erich Vásquez Delgado3 , Daniel Jeremy Pósito Díaz3
, Daniel Jeremy Pósito Díaz3 Janett Ignacia
Vásquez Julca3
Janett Ignacia
Vásquez Julca3 , Segundo Gerson Ugkum Samekash3
, Segundo Gerson Ugkum Samekash3
RESUMEN
El
objetivo de esta investigación fue revalorar los saberes matemáticos que se
evidencian en la cerámica awajún y vincularlos como estrategia lúdica para la
enseñanza de la hidráulica de canales en los estudiantes de ingeniería civil de
la Universidad Nacional Intercultural “Fabiola Salazar Leguía” de Bagua. La
metodología empleada consistió en realizar estudios observacionales y
descriptivos. La pertinencia del enfoque radica en describir las prácticas
ancestrales y costumbres de una determinada comunidad con relación a su
contexto cultural. La investigación se desarrolló en tres etapas: i) Revisión
documentaria, así como fuentes de información gráfica y virtual de la cerámica
awajún. ii) Se recolectaron muestras de la cerámica awajún y realización de entrevistas
a pobladoras awajún. iii) Se elaboraron perfiles de canales hidráulicos cuya
referencia son las figuras geométricas que aparecen en la cerámica awajún
moldeadas en piezas del tangram. Asimismo, se digitalizó algunos diseños de
cerámicas. Los resultados obtenidos fueron la sistematización de la información
respecto a los insumos empleados para la elaboración de las cerámicas awajún,
además la identificación de las figuras geométricas que aparecen de forma
recurrente en esta cerámica, principalmente en las piníg y amamuk. Se concluye
que, en la cerámica awajún se evidencia que sus pobladores poseen un
conocimiento elemental de la geometría, principalmente del círculo, triángulo y
las líneas. y que, haciendo uso de las piezas del tangram, tomando como base el
triángulo de las figuras geométricas de la cerámica awajún, se demuestra que el
radio hidráulico es el mejor en condiciones de canal trapezoidal.
Palabras claves: Cerámica
awajún, etnomatemática, hidráulica, tangram.
ABSTRACT
The objective of this research is to reassess the
mathematical knowledge that is evidenced in Awajún ceramics and link them as a
playful strategy for teaching canal hydraulics to civil engineering students of
the "Fabiola Salazar Leguía" National Intercultural University of Bagua.
The methodology used consisted of conducting observational and descriptive
studies. The relevance of the approach lies in describing the ancestral
practices and customs of a given community in relation to its cultural context.
The research was developed in three stages: i) Documentary review, as well as
graphic and virtual sources of information on Awajún ceramics. ii) Samples of
Awajún ceramics were collected and interviews were conducted with Awajún women.
iii) Profiles of hydraulic channels were elaborated whose reference are the
geometric figures that appear in the Awajún ceramics molded in pieces of the
tangram. Likewise, some ceramic designs were digitized. The results obtained
were the systematization of the information regarding the inputs used for the
elaboration of the Awajún ceramics, as well as the identification of the
geometric figures that appear recurrently in this ceramic, mainly in the piníg
and amamuk. It is concluded that, in the Awajún ceramics, it is evident that
its inhabitants have an elementary knowledge of geometry, mainly of the circle,
triangle and lines. and that, using the pieces of the tangram, based on the
triangle of the geometric figures of Awajún pottery, it is shown that the
hydraulic radius is the best in trapezoidal channel conditions.
Keywords: Awajún pottery,
ethnomathematics, hydraulics, tangram.
1 Docente de la Universidad Nacional
Intercultural “Fabiola Salazar Leguía” de Bagua-Perú, correo: restela@unibagua.edu.pe
2Docente de la I.E Túpac Amaru de
Chiriaco-Amazonas-Perú, correo: elisacontbar@gmail.com
3Estudiante de Ingeniería Civil de la
Universidad Nacional Intercultural “Fabiola Salazar Leguía” de Bagua-Perú,
correo: jvasquezd@unibagua.edu.pe, dposito@unibagua.edu.pe, jvasquezi@unibagua.edu.pe, sugkums@unibagua.edu.pe
RESUMO
O objetivo desta pesquisa é reavaliar os conhecimentos
matemáticos evidenciados na cerâmica Awajún e vinculá-los como uma estratégia
lúdica para o ensino de hidráulica de canais para estudantes de engenharia
civil da Universidade Nacional Intercultural "Fabiola Salazar Leguía"
de Bagua. A metodologia utilizada consistiu na realização de estudos
observacionais e descritivos. A relevância da abordagem está em descrever as
práticas e costumes ancestrais de uma determinada comunidade em relação ao seu
contexto cultural. A pesquisa foi desenvolvida em três etapas: i) Revisão
documental, bem como fontes gráficas e virtuais de informação sobre a cerâmica
Awajún. ii) Amostras de cerâmica Awajún foram coletadas e entrevistas foram
realizadas com mulheres Awajún. iii) Foram elaborados perfis de canais
hidráulicos cuja referência são as figuras geométricas que aparecem nas
cerâmicas Awajún moldadas em peças do tangram. Da mesma forma, alguns desenhos
cerâmicos foram digitalizados. Os resultados obtidos foram a sistematização das
informações referentes aos insumos utilizados para a elaboração da cerâmica
Awajún, bem como a identificação das figuras geométricas que aparecem
recorrentemente nesta cerâmica, principalmente no piníg e amamuk. Conclui-se
que, na cerâmica Awajún, é evidente que seus habitantes possuem um conhecimento
elementar de geometria, principalmente do círculo, triângulo e linhas. e que,
usando as peças do tangram, baseado no triângulo das figuras geométricas da
cerâmica Awajún, mostra-se que o raio hidráulico é o melhor em condições de
canal trapezoidal.
Palavras-chave: Cerâmica Awajún, etnomatemática, hidráulica,
tangram.
INTRODUCCIÓN
Los pobladores awajún se encuentran ubicados en las
regiones de Amazonas, Loreto y en la zona norte de San Martín y Cajamarca,
constituyéndose como el segundo más poblado de la Amazonía peruana y la
identificación cultural de sus integrantes ha permitido que se distingan de
otros grupos amazónicos (Ministerio de Cultura del Perú, 2015). Es importante
hacer una distinción de dos expresiones que suelen confundirse: “pueblo
indígena” referido a los pobladores que comparten un territorio común, por otro
lado “comunidad nativa”, representan las familias que derivan de un pueblo
indígena (Inoach, 2021).
Los pobladores amazónicos afianzan sus vivencias,
experiencias, así como su saber ancestral y creencias por medio de la identidad
cultural (Inoach, 2021). Es en este contexto que, el pueblo awajún muestra su
acción creadora y estética por medio de la elaboración de piezas de cerámicas.
Esta expresión artística es realizada por las mujeres, cuyo conocimiento se
transmite de generación en generación. De esta manera, se conserva su saber
ancestral y se fortalece su identidad cultural (Ministerio de Cultura del Perú,
2015). El saber ancestral awajún reflejado en su cerámica representa un insumo
para el análisis académico, sobre todo en el ámbito de las relaciones
matemáticas, y la presencia de figuras geométricas elementales recurrentes.
Este “saber geométrico” del poblador awajún alejado de todo academicismo
permite revalorarlos y traerlos a contexto en la formación de un futuro profesional,
donde no solo se desarrolla un aprendizaje, sino un intercambio de experiencias
a través de un diálogo cultural (Olivas et al., 2016).
El flujo hidráulico por efecto gravitatorio, es
decir a diferencias de cotas topográficas y en conductos abiertos, suelen
llamarlos canales naturales o sin revestir; y aquellos cuya superficie es
revestida se le denomina canales artificiales (Mejía & Benavides, 2017). La
expresión matemática que relaciona los elementos geométricos de un canal es la
fórmula de Manning, cuyo modelo se sustenta en características físicas e
hidráulicas del conducto como: ancho de base, pendiente del terreno, rugosidad
del material, talud, espejo de agua, tirante de agua (Aldama & Ocón, 2002).
El flujo del líquido en un canal hidráulico lleva a
la determinación de su caudal (Q) que representa el volumen por unidad de
tiempo cuya unidad de medida es (m^3/s). La metodología empleada es mediante el
método de aforo. Este consiste en calcular el tiempo de recorrido de un objeto
flotador teniendo en cuenta la sección transversal del canal (Mejía &
Benavides, 2017). La determinación del caudal y la velocidad del flujo están
relacionadas por la ecuación de continuidad, cuya explicación hidráulica es la
conservación de la masa (Castellanos et al., 2017).
El génesis del término etnomatemática está
estrechamente relacionada a la incursión de la etnografía en la ciencia,
fundamentalmente de la matemática, donde se incorpora la realidad contextual en
un proceso de enseñanza aprendizaje (Saumell, 2021). La historiografía de la
matemática evidencia que la variedad temática de muchos programas de estudio va
más allá del contenido occidentalizado, sino todo lo contrario una matemática
universal, y por decirlo de algún modo, patrimonio de la humanidad. Los
pueblos, en toda su historia, aportan para universalizar la matemática. El
enriquecimiento de los saberes impartidos no es estático, sino que se alimentan
de las actividades culturales de ellos mismos (Ministerio de Educación del
Perú, 2013).
La matemática es considerada una asignatura
“difícil”, cuya comprensión es percibida como compleja por su alto nivel de
abstracción. En este sentido, la tendencia en la actualidad es desarrollar la
asignatura desde procesos culturales (Saumell, 2021). Es decir, la
etnomatemática constituye la técnica para explicar un contenido que no solo se
restringe a cuantificar sino hasta la modelación, haciendo uso de su contexto
cultural y sus actividades culturales (Micelli & Crespo, 2011). Poner en
valor los saberes ancestrales de una comunidad al incorporarlos a los planes de
estudio permite la democratización de su cultura, no solo a nivel de la
enseñanza en el aula, sino también desde el campo de la investigación (Fuentes,
2014).
El dékamu o conocimiento que poseen las pobladoras
awajún es indiscutiblemente entre otras actividades la elaboración de cerámica
tradicional. Esta actividad consiste en el proceso de transformación de los
insumos que la naturaleza le provee como resinas, cenizas, arcillas y hojas.
Estos materiales se convierten en tintes, marcadores, así como la masa blanda
que permite moldear e imprimir su saber y actividades cotidianas, y cuyo legado
se viene conservando de generación en generación. Los elementos que ahora se
consideran “estandarizados” para la elaboración de cerámica awajún es el
resultado de un proceso de aprendizaje y experimentación, donde el bosque
amazónico constituye el proveedor esencial en la etapa creadora de la mujer
awajún (Ministerio de Cultura del Perú, 2015). Los utensilios utilizados por
las ceramistas awajún, así como los diversos materiales e insumos son
seleccionados directamente del bosque, de esta forma plasman su cosmovisión y
saber ancestral (Nolte, 2021).
El Tangram es un juego que está conformado por 7
figuras poligonales, constituyendo estas un rompecabezas. Su origen se remonta
al continente asiático, y se le conoce como “rompecabezas de transformación”.
Este juego se compone de 5 triángulos rectos, una figura cuadrada y un
paralelogramo (Scribano, 2020). Se pueden formar variedad de figuras con estas
piezas base, cuya utilidad y mayor uso se remonta a la educación básica regular
en el proceso de enseñanza aprendizaje, sobre todo para afianzar a este nivel
habilidades múltiples, pero sobre todo las habilidades geométricas en los
educandos (Espinosa & León, 2019).
El tangram como juego permite establecer retos donde
se evidencia las habilidades aritméticas y geométricas, ya que las piezas deben
ubicarse de manera tal que, el común sea la superficie de la figura
diferenciándose en el perímetro de la misma. Estas actividades lúdicas en los
espacios de enseñanza-aprendizaje fomentan la participación activa de los
estudiantes (Espinosa & León, 2019).
El objetivo de la presente investigación fue revalorar
los saberes matemáticos que se evidencian en la cerámica awajún y vincularlos
como estrategia lúdica para la enseñanza de la hidráulica de canales a los
estudiantes de ingeniería civil de la Universidad Nacional Intercultural
“Fabiola Salazar Leguía” de Bagua.
MATERIALES Y MÉTODOS
Se realizaron estudios observacionales y descriptivos (Huapaya &
Salas, 2008). La pertinencia del enfoque radica en describir las practicas
ancestrales y costumbres de una determinada comunidad con relación a su
contexto cultural (Castro et al., 2020).
La investigación se desarrolló en tres etapas: i) Revisión
documentaria, así como fuentes de información gráfica y virtual (Pamplona et
al., 2019) de cerámica awajún. ii) Se recolectaron muestras de cerámica awajún
y realización de entrevistas a pobladoras awajún. iii) Se hicieron perfiles de
canales hidráulicos cuya referencia son las figuras geométricas que aparecen en
la cerámica awajún moldeadas en piezas del tangram, Asimismo, se digitalizó
algunos diseños de cerámicas (Rodríguez, 2021).
En nuestra indagación se utilizó la metodología
cualitativa (Sánchez et al., 2019) con la finalidad de recabar información de
primera mano por medio de entrevistas (Tabla 1). De esta manera, permitió la
constante observación y la interrelación con los mismos pobladores (Ordinola et
al., 2019).
Tabla 2. Preguntas realizadas a pobladoras
amazónicas awajún
|
Inibau (awajún)
|
Pregunta (español)
|
|
Dajish yaita?
|
¿Cuál es su nombre?
|
|
yamaiyanish wajupa mijanta ajawa?
|
¿Qué edad tiene actualmente?
|
|
wajuk batsatkamunmaya amazonashnumiash
minawa?
|
¿De qué comunidad amazónica proviene?
|
|
Yaki jintintuawami duwejai najantai
aidaunash?
|
¿Quién le enseñó el arte de elaborar
cerámica?
|
|
wajupa mijanta ajuyi duwejai takatai
jintinbaunmash?
|
¿Cuántos años tenía cuando le enseñaron
a elaborar cerámica?
|
|
waji atsumtaiyaita duwejai takat aidau
najanbaunmash?
|
¿Qué insumos necesita para la
elaboración de cerámica?
|
|
augmattsata wajuk nagkamsaish
najantaiyaita dewejai najantai awajundau aidaush
|
Describa como es el proceso de
elaboración de la cerámica awajún
|
|
tuwi jutaiyaita duwejai najanku takatai
aidaush?
|
¿Dónde consigue esos insumos?
|
|
Wajinma atsumtaita duwejai takatai
najankamu aidaush?
|
¿Cuál es la utilidad de los cerámicos?
|
|
wajina iwainawa duwejai najankamunun
agakbau aina dusha?
|
¿Qué representa las inscripciones en la
cerámica?
|
|
Juju takatnash aishmagkush takamainkaik?
|
¿Esta actividad la puede realizar un
varón?
|
|
Wajupa tsawanta megkaewa duwejai
najantai aidaun najanatasash?
|
¿Cuánto tiempo emplea para elaborar una
cerámica?
|
La revisión de cerámica awajún fue realizada de manera presencial con
algunas piezas mostradas por pobladores de la comunidad de Tutumberos, y
algunas piezas se revisaron por medio de sesiones virtuales durante el curso de
métodos numéricos. La caracterización de las cerámicas se hizo teniendo en
cuenta las figuras geométricas elementales que aparecen (Beltrón et al., 2019).
Se informó a los estudiantes y a los entrevistados
respecto al uso de los datos obtenidos, que responden directamente a los
objetivos de nuestra investigación (Unda, 2020).
Las fuentes de información documentaria, gráfica y
virtual de cerámica awajún. Se sistematizó la información como resultado de la
revisión de artículos científicos, libros y ejemplares de cerámicos awajún,
rescatando los elementos geométricos que se muestran en los cerámicos.
Tabla
1.
Sistematización de la información revisada y muestras de cerámicas awajún
|
Foto de la cerámica -piníg y amamuk
|
Descripción del elemento geométrico más notorio
|
|

|
Línea quebrada
|
|

|
Triángulos equiláteros
|
|

|
Círculos concéntricos
|
|

|
Línea recta
|
|

|
Cuadrilátero - Paralelogramo
|
|

|
Triángulos equiláteros
|
|

|
Líneas rectas secantes
|
|

|
Polígonos estrellados
|
Como resultado de las entrevistas sostenidas a
pobladoras awajún se consolidó los principales insumos empleados por ellas en
la elaboración de la cerámica, y que es obtenida directamente del bosque
amazónico (Tabla 2).
Tabla
2. Principales
insumos utilizados por las pobladoras amazónicas awajún
|
Nombre del insumo en awajun
|
Utilidad
|
Descripción
|
|
Chígkim
|
cocción de las piezas de cerámica
|
Leña de árboles también se suelen usar
cáscaras
|
|
Majág
|
teñir
|
Arcilla de color rojiza y amarillo
|
|
Yukáip
|
sellar
|
Sellado y barnizado de la cerámica
|
|
kayushik agantin
|
dibujar
|
Carbón de cualquier madera para dibujar diseños
|
|
Ipak
|
teñir
|
Achiote se emplea para pintar de rojo
|
|
Dúwe
|
masa
|
Barro húmedo y flexible
|
|
Yukuúku
|
ceniza
|
Mezcla con el dúwe para darle
resistencia
|
Las entrevistas a las pobladoras awajún fueron
realizadas por los estudiantes de ingeniería civil de la UNIFSLB del quinto
ciclo de estudios durante el curso de métodos numéricos. Estas entrevistas
consistieron en una fase de consenso y depuración de preguntas con la finalidad
de obtener información relevante para el cumplimiento de los objetivos (Figura
1).
Figura
1.
Estudiantes de Ingeniería civil realizando la entrevista a pobladora awajún
Se hicieron perfiles de canales hidráulicos tomando
como base figuras geométricas que aparecen en la cerámica awajún tomando como
base las piezas del tangram, así como la digitalización de cerámicas.
Los estudiantes procedieron a realizaron el análisis
geométrico de los perfiles de las secciones transversales en la hidráulica de
canales: Canal triangular, rectangular y trapezoidal (Figura 2).
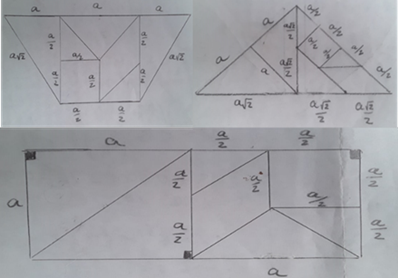
Figura
2.
Resultado de los análisis geométricos de tres perfiles de canales hidráulicos
con piezas tangram
Los elementos geométricos de un canal hidráulico
definen variables de gran importancia para el ingeniero civil como es el caudal
y la velocidad del flujo. Área hidráulica en base al uso de las figuras del
tangram representa numéricamente la misma cantidad en los tres casos antes
mencionados (Figura 3).
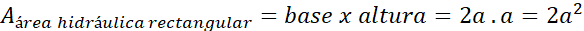
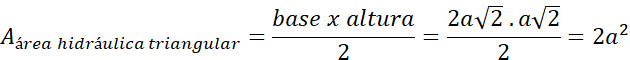


Figura 3.
Estudiantes de Ingeniería civil utilizando las piezas del tangram para el
cálculo de radio hidráulico
El perímetro mojado representa la sumatoria de
contornos de las figuras seleccionadas, y se evidencia que en los tres casos
anteriores resulta cantidades diferentes (Figura 4).
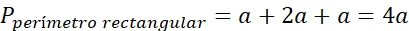
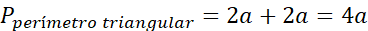
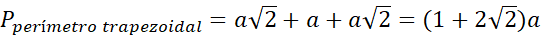
Figura
4. Análisis geométricos de tres
perfiles de canales hidráulicos con piezas tangram
El uso de las piezas del tangram nos permite
determinar el radio hidráulico de los canales mencionados
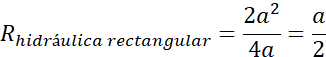
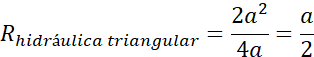

Estrategia que permitió
demostrar de manera lúdica que el mayor radio hidráulico la posee la sección
trapezoidal (Figura 5). Se codificaron programas en lenguaje Python con la
finalidad de replicar la simetría y periodicidad de sus formas de la pinig y
amamuk a las que tuvimos acceso de manera física o documentaria.
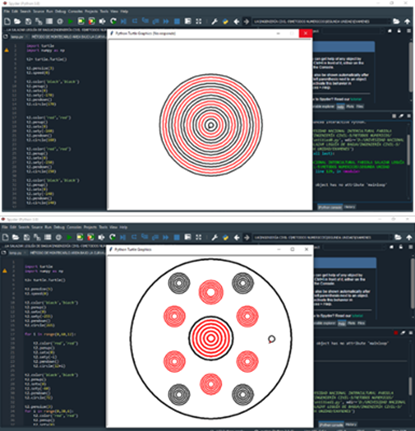
Figura 5.
Digitalización de diseños de la cerámica awajún en lenguaje programación Python
DISCUSIÓN
Existe una resistencia a incorporar las vivencias
culturales ancestrales a la enseñanza de la matemática en el aula. Por ello, se
torna difícil romper los paradigmas respecto al currículo rígido y a la no
interculturalidad en materias que requieren un mayor nivel de abstracción
(Alarcón & Flores, 2021). Sin embargo, el esfuerzo de muchos maestros tanto
de nivel básico como universitario para proponer y poner en práctica
experiencias innovadoras en la enseñanza de geometría, se convierte en una
estrategia para revalorar conocimientos o saberes culturales, inclusive
haciendo uso de herramientas digitales para su enseñanza (Ruiz, 2009). La
evidencia demuestra que los pobladores originarios, a pesar de no poseer una
formación académica en temas matemáticos, no han significado una limitante para
que ellos puedan replicar y difundir a sus descendientes los
conocimientos ancestrales que se visualizan como
expresión de su arte. A través de la creación de sus cerámicos o textiles se
exhiben grabados que muestran la utilización de un lenguaje matemático en sus
actividades cotidianas (García, 2007). La ponderación histórica y cultural que
representa traer a vigencia curricular estos conocimientos ancestrales permite
que nuestra propia cultura se nutra, y la temática encuentre pertinencia en los
estudiantes (Micelli & Crespo, 2011).
El uso de actividades que permitan la manipulación
de material concreto en sesiones de aprendizaje, como es el caso de piezas del
tangram, ha evidenciado que los niños, adolescentes o jóvenes se puedan
apropiar de temáticas referidas a la geometría plana sin necesidad de
abrumarlos con teoremas o teorías profundas, todo lo contrario, representa un
aprendizaje en el juego (Espinosa & León, 2019). Procedimientos como:
observar, definir, esquematizar, proponer y dar solución a situaciones
problemáticas se pueden abordar con estudiantes desde educación básica regular
en la medida que puedan ser estimulados apropiadamente con estrategias de
aprendizaje en entornos lúdicos (Camargo, 2011).
Una pedagogía en movimiento es la etnomatemática, es
un reto para el maestro actual que pueda incorporar las manifestaciones
sociales, culturales y todas las actividades del quehacer, tanto del individuo
como el colectivo, para integrarlos como elementos de su sesión de aprendizaje
generando expectativa en el estudiante (D’Ambrosio, 2014). La relación contexto
- asignatura representa un valor agregado a las estrategias didácticas que el
docente esgrime al momento de desarrollar su materia. La historia y la cultura
deben estar conectadas con la etnomatemática, de tal forma que, el bagaje del
docente se ve enriquecido para la propuesta de nuevas estrategias que se
orientan a mejorar el proceso de enseñanza aprendizaje con tolerancia cultural
(Huapaya & Salas, 2008).
Una mirada atenta a las ocupaciones u oficios del
entorno podría resultar aleccionador para el docente, por ejemplo, la actividad
matemática que desarrollan los maestros constructores o los albañiles, quienes
de muchas y continuas formas hacen uso del cálculo aritmético, geométrico y
trigonométrico, resultará de fácil imagen para un estudiante del uso de las
matemáticas en la vida diaria (Rey & Aroca, 2011). El uso de dispositivos
electrónicos modernos o nuevas tecnologías, de alguna forma está postergando y
casi extinguiendo, la posibilidad de mostrar al estudiante las prácticas
ancestrales de cálculo de distancias, ubicación o formas prácticas de
estimaciones aritméticas como la estatura de una persona o la altura de un
árbol en función de su sombra (Regan, 2020). Las comunidades o pueblos originarios
construyen su historia y cultura en base a códigos que pueden evidenciarse en
gestos o emociones, que de alguna manera el docente y estudiante están
dispuestos a interiorizar para construir ciencia con ese contexto, de tal
manera que el lenguaje científico permanece en respeto y aceptación cultural
(Blanco et al., 2017).
CONCLUSIONES
Las pobladoras awajún obtienen los insumos empleados
para la elaboración de la cerámica awajún directamente del bosque amazónico.
En la cerámica awajún principalmente en las piníg y
amamuk, se evidencia que el poblador awajún posee un conocimiento elemental de
la geometría, principalmente del círculo, triángulo y las líneas.
Utilizando las piezas del tangram, tomando como base
el triángulo de las figuras geométricas de la cerámica awajún, se demuestra que
el radio hidráulico es el mejor en condiciones de canal trapezoidal.
REFERENCIAS
BIBLIOGRÁFICAS
Alarcón, R., & Flores, H. (2021).
Aplicación de algoritmos etnomatemáticos en el aprendizaje significativo de
estudiantes universitarios. INNOVA Research Journal, 6(1), 195–215.
https://doi.org/10.33890/innova.v6.n1.2021.1522
Aldama, Á., & Ocón, A.
(2002). Resistencia al
flujo en canales y límites de aplicabilidad de la fórmula de Manning.
Ingenieria Hidraulica En Mexico, 17(1), 107–115.
http://repositorio.imta.mx/handle/20.500.12013/752
Beltrón, J., Hernández, L., &
Carrasco, T. (2019). Competencia modelación matemática: concepciones y
situación diagnóstica en carreras de Ingeniería. Revista Cubana de Educación
Superior, 38(2), 1–12.
http://scielo.sld.cu/scielo.php?script=sci_abstract&pid=S0257-43142019000200005&lng=es&nrm=iso
Blanco, H., Fernández, A., &
Oliveras, M. (2017). Formación de Profesores de Matemáticas desde la
Etnomatemática: Estado de desarrollo. Bolema - Mathematics Education Bulletin, 31(58),
564–589. https://doi.org/10.1590/1980-4415v31n58a02
Camargo, L. (2011). El legado de Piaget a la didáctica de
la Geometría. Revista Colombiana de Educación, 60, 41–60.
https://doi.org/10.17227/01203916.840
Castellanos, H., Collazos, C.,
Farfan, J., & Meléndez, F. (2017). Diseño y construcción de un canal
hidráulico de pendiente variable. Informacion Tecnologica, 28(6), 103–114.
Castro, A., Rodríguez, C., Aravena,
L., Loncomilla, A., & Pizarro, D. (2020). Nociones matemáticas evidenciadas
en la práctica cotidiana de un carpintero del sur de Chile. Revista Científica,
39(3), 278–295. https://doi.org/10.14483/23448350.16270
D’Ambrosio, U. (2014). Las bases
conceptuales del Programa Etnomatemática. Revista Latinoamericana de
Ethnomatemática, 7(2), 100–107.
http://www.redalyc.org/articulo.oa?id=274031870007
Espinosa, J., & León, J. (2019).
Propuesta para la elaboración y utilización del Tangram y el geoplano en el
proceso de enseñanaza-aprendizaje de la geometría de la educación infantil.
Revista Conrado, 15(69), 181–186.
http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1990-86442019000400181
Fuentes, C. (2014). Algunos enfoques
de investigación en Etnomatemática. Revista Latinoamericana de Etnomatemática,
7(1), 155.
https://www.revista.etnomatematica.org/index.php/RevLatEm/article/view/107
García, J. (2007). Conocimientos
geométricos en la elaboración de un artefacto en una comunidad ñuu savi.
Revista de Investigación Educativa de La REDIECH, 10(19), 105–120. https://doi.org/10.33010/ie_rie_rediech.v10i19.634
Huapaya, E., & Salas, C. (2008).
Uso de las ideas matemáticas y científicas de los Incas, en la
enseñanza-aprendizaje de la geometría. Revista Latinoamericana de
Etnomatemática,1(1),4–11.
Inoach, G. (2021). Proceso de
constitución del gobierno territorial autónomo awajún. Revista Amazonía
Peruana, 17(34), 13–29. https://doi.org/10.52980/revistaamazonaperuana.vi34.256
Mejía, D., & Benavides, H.
(2017). Cálculo del coeficiente de rugosidad “n” para canales trapezoidales con
presencia de sedimento (Ø = 0.05 mm). Tecnocienca Chihuahua, XI(2), 69–81. https://vocero.uach.mx/index.php/tecnociencia/artic
Micelli, M., & Crespo, C. (2011).
La Geometría Entretejida. Revista Latinoamericana de Ethnomatemática, 4(1),
4–20. https://www.redalyc.org/articulo.oa?id=274019440001
Ministerio de Cultura del Perú.
(2015). Cerámica tradicional awajún. www.cultura.gob.pe
Ministerio de Educación del Perú.
(2013). Geometría y Cestería de los Bora en la Amazonía Peruana. www.minedu.gob.pe
Nolte, J. (2021). Gráfica
awajún : geometría del universo (Primera). KWY Ediciones de Musuk Nolte.
Olivas, R., Mancera, F., &
Romero, R. (2016). La etnomatemática: los saberes matemáticos de los pueblos
originarios. RECIE. Revista Electrónica Científica de Investigación Educativa,
3(1), 123–136. https://www.rediech.org/ojs/2017/index.php/re
Ordinola, C., Barrena, M., Gamarra,
O., Rascón, J., Corroto, F., Taramona, L., & Mejía, F. (2019). Creencias y
costumbres de madres y parteras para la atención del embarazo, parto y
puerperio en el distrito de Huancas (Chachapoyas, Perú). Arnaldoa, 26(1),
325–338. https://doi.org/10.22497/arnaldoa.261.26115
Pamplona, J., Cuesta, J., & Cano,
V. (2019). Estrategias De Enseñanza Del Docente En Las Áreas Básicas: Una
Mirada Al Aprendizaje Escolar. Revista Eleuthera, 21, 13–33.
https://doi.org/10.17151/eleu.2019.21.2
Regan, J. (2020). Territorio, género
y construcción de canoas entre los awajún-shuar y los kokama-omagua. Amazonia
Peruana, 17(33), 147–162.
https://doi.org/10.52980/revistaamazonaperuana.vi33.23
Rey, M., & Aroca, A. (2011).
Medición y estimación de los albañiles, un aporte a la educación matemática.
Revista U.D.C.A Actualidad & Divulgación Científica, 14(1), 137–147.
http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0123-42262011000100017&lang=pt%0Ahttp://www.scielo.org.co/pdf/rudca/v14n1/v14n1a17.pdf
Rodríguez, C. (2021). Conexiones
etnomatemáticas entre conceptos geométricos en la elaboración de las tortillas
de Chilpancingo, México. Revista de Investigación, Desarrollo e Innovación,
11(2), 273–296. https://doi.org/10.19053/20278306.v11.n2.2021.12756
Ruiz, N. (2009). Medios y recursos
para la enseñanza de la geometría en la educación obligatoria. Revista de
Didácticas Específicas, 3, 8–24. https://revistas.uam.es/didacticasespecificas/art
Sánchez, M., García, J., Steffens,
E., & Hernández, H. (2019). Estrategias Pedagógicas en Procesos de
Enseñanza y Aprendizaje en la Educación Superior incluyendo Tecnologías de la
Información y las Comunicaciones.
Información Tecnológica, 30(3),
277–286. https://doi.org/10.4067/s0718-07642019000300277
Saumell, N. (2021). La
etnomatemática. Su importancia para un proceso de enseñanza aprendizaje con
significación social y cultural. Revista Conrado, 17(82), 1-103–110.
https://conrado.ucf.edu.cu/index.php/conrado/article/view/1937/1896
Scribano, A. (2020). La vida como
Tangram : Hacia multiplicidades de ecologías emocionales. Revista
Latinoamericana de Estudios Sobre Cuerpos, Emociones y Sociedad, 33(12), 4–7.
http://www.relaces.com.ar/index.php/relaces/article/view/2
Unda, F. (2020). Interacciones
docentes-estudiantes y prácticas sexistas en el aula del sistema de educación
intercultural bilingüe. Revista Scientific, 5(15), 129–149.
https://doi.org/10.29394/Scientific.issn.2542-2987.2020.5.15.6.129-149
![]() *, Elisa
Contreras Barsallo2
*, Elisa
Contreras Barsallo2![]() Jean
Erich Vásquez Delgado3
Jean
Erich Vásquez Delgado3![]() , Daniel Jeremy Pósito Díaz3
, Daniel Jeremy Pósito Díaz3![]() Janett Ignacia
Vásquez Julca3
Janett Ignacia
Vásquez Julca3![]() , Segundo Gerson Ugkum Samekash3
, Segundo Gerson Ugkum Samekash3![]()












