Etnomatem tica: Alba iles y los procesos
constructivos en Bagua-Amazonas
Ethnomathematics:
Masons and construction processes in Bagua-Amazonas
Etnomatem tica:
Pedreiros e processos construtivos em Bagua-Amazonas
Ronald Omar Estela Urbina , Elisa Contreras Barsallo
, Elisa Contreras Barsallo ,
Alcides Ra l Cuti Gutierrez
,
Alcides Ra l Cuti Gutierrez
Juan
Percy Mamani Cutipa , Carlos
Carcausto Quispe4
, Carlos
Carcausto Quispe4 , Giovanna
Guzm n C ceres
, Giovanna
Guzm n C ceres
Segundo
Leonardo Valdivia Velasquez3 , Edinson
Figueroa Fern ndez1
, Edinson
Figueroa Fern ndez1 ,
Luis Miguel Villegas Santamar a
,
Luis Miguel Villegas Santamar a
DOI:
https://doi.org/10.55996/dekamuagropec.v5i1.212
RESUMEN
El objetivo de esta investigaci n fue
profundizar en la comprensi n de la etnomatem tica desarrollada por los
alba iles en las regiones amaz nicas del Per . Para ello, se identific y
analiz los conceptos matem ticos impl citos en las pr cticas de los alba iles,
as como comprender el papel de la cultura y el entorno natural en la
configuraci n de este conocimiento. El tipo de estudio se consider
etnogr fico, consisti en recabar informaci n, previa observaci n. Se aplic un
cuestionario, con la finalidad de evidenciar los procedimientos que realizan
los alba iles en la resoluci n de c lculos laborales empleando las operaciones
fundamentales (suma, resta, multiplicaci n y divisi n) de origen
etnomatem tico. De la misma forma, se revis art culos cient ficos. Uno de los
hallazgos clave de esta investigaci n es la integraci n de conceptos
matem ticos en la pr ctica laboral de los alba iles. Se observ c mo estos
trabajadores utilizan una amplia gama de conceptos, desde la geometr a hasta el
c lculo, en la planificaci n y ejecuci n de sus tareas diarias. Esta
integraci n demostr que las matem ticas no son un concepto abstracto separado
de la vida cotidiana, sino una herramienta pr ctica y tangible que se utiliza
de manera efectiva para resolver problemas concretos.
Palabras
claves: alba il, cultural, etnogr fica, etnomatem tica.
ABSTRACT
The objective of this research was to deepen the understanding of ethnomathematics developed by masons in the Amazonian regions of Peru. To this end, the mathematical concepts implicit in the masons' practices were identified and analyzed, as well as to understand the role of culture and the natural environment in the configuration of this knowledge. The type of study was considered ethnographic, and consisted of gathering information through observation. A questionnaire was applied, with the purpose of evidencing the procedures carried out by the masons in the resolution of labor calculations using the fundamental operations (addition, subtraction, multiplication and division) of ethnomathematical origin. In the same way, scientific articles were reviewed. One of the key findings of this research is the integration of mathematical concepts in the labor practice of masons. It was observed how these workers use a wide range of concepts, from geometry to calculus, in the planning and execution of their daily tasks. This integration demonstrated that mathematics is not an abstract concept separated from everyday life, but a practical and tangible tool that is used effectively to solve concrete problems.
Keywords: bricklayer, cultural, ethnographic, ethnomathematical.
RESUMO
O objetivo desta investiga o foi o de aprofundar o conhecimento
da etnomatem tica desenvolvida pelos pedreiros nas regi es amaz nicas do Peru.
Para o efeito, identific mos e analis mos os conceitos matem ticos impl citos
nas pr ticas dos pedreiros, bem como para compreender o papel da cultura e do
ambiente natural na configura o destes conhecimentos. O tipo de estudo foi
considerado etnogr fico e consistiu na recolha de informa es atrav s da
observa o. Foi aplicado um question rio, com o objetivo de mostrar os
procedimentos realizados pelos pedreiros na resolu o de c lculos de trabalho
utilizando as opera es fundamentais (adi o, subtra o, multiplica o e
divis o) de origem etnomatem tica. Da mesma forma, foram analisados artigos cient ficos.
Uma das principais conclus es desta investiga o a integra o de conceitos
matem ticos na pr tica profissional dos pedreiros. Observou-se como estes
trabalhadores utilizam uma vasta gama de conceitos, desde a geometria ao
c lculo, no planeamento e execu o das suas tarefas di rias. Esta integra o
demonstrou que a matem tica n o um conceito abstrato separado da vida
quotidiana, mas uma ferramenta pr tica e tang vel que utilizada eficazmente
para resolver problemas concretos.
Palavras-chave:
pedreiro, cultural, etnogr fico, etnomatem tico.
INTRODUCCI N
Las vastas y exuberantes regiones amaz nicas
del Per son hogar de una biodiversidad incomparable, no solo en t rminos de
flora y fauna, sino tambi n en cuanto a la riqueza cultural de las comunidades
que las habitan (Estela et
al., 2021). Dentro de este
contexto de diversidad, las pr cticas matem ticas de los alba iles emergen como
un aspecto fascinante y fundamental de la vida cotidiana en estas regiones (Pereira, 2019). Este estudio se propone adentrarse en el intrincado
entramado de la etnomatem tica desarrollada por los alba iles en las regiones
amaz nicas del Per , explorando c mo estas pr cticas reflejan no solo la
habilidad t cnica de los trabajadores, sino tambi n su profunda comprensi n
matem tica arraigada en el contexto cultural y ambiental de la selva (Aroca, 2022).
Las regiones amaz nicas del Per , conocidas por
su densa vegetaci n, r os serpenteantes y una diversidad cultural asombrosa,
han sido hogar de diversas comunidades ind genas durante milenios. Estas
comunidades han desarrollado sistemas de conocimiento intrincados que les han
permitido adaptarse y sobrevivir en este entorno desafiante. Desde la
navegaci n fluvial hasta la agricultura sostenible, las pr cticas cotidianas de
estas comunidades est n impregnadas de una profunda comprensi n del entorno
natural y los recursos disponibles.
Dentro de este contexto de conocimiento
arraigado en la naturaleza, los alba iles se destacan como figuras centrales en
la creaci n y transformaci n del entorno construido en las regiones amaz nicas
del Per . Estos h biles artesanos no solo dominan las t cnicas de construcci n,
sino que tambi n aplican una variedad de conceptos matem ticos en su trabajo
diario. Desde la planificaci n y dise o de estructuras hasta la distribuci n de
materiales y la estimaci n de costos, los alba iles dependen de una comprensi n
profunda de las matem ticas para llevar a cabo sus tareas de manera eficiente y
precisa.
La etnomatem tica, como campo
interdisciplinario, nos ofrece una lente a trav s de la cual podemos examinar y
comprender las pr cticas matem ticas de los alba iles en un contexto cultural y
ambiental espec fico (Morales & Rodr guez,
2022). Al adoptar un enfoque etnogr fico y participativo, este estudio
busca explorar c mo los alba iles aplican y desarrollan el pensamiento
matem tico en su trabajo, as como comprender la influencia del contexto
cultural y ambiental en estas pr cticas (Alsina,
2019).
La etnomatem tica es un campo de estudio que
busca entender y valorar las diversas formas en que diferentes culturas aplican
y desarrollan el pensamiento matem tico en sus contextos cotidianos (Barrios et al., 2022). Dentro de este campo, los alba iles destacan
como figuras cuyo trabajo no solo implica la construcci n de edificaciones
f sicas, sino tambi n la aplicaci n de conceptos matem ticos complejos en su
quehacer diario (Rodr guez,
2021). Este estudio se propone explorar en
profundidad la etnomatem tica de los alba iles, examinando c mo estas pr cticas
reflejan su comprensi n nica de las matem ticas en su contexto laboral y
cultural.
Los alba iles son trabajadores fundamentales en
la industria de la construcci n, responsables de erigir y mantener estructuras
que forman la base de la sociedad moderna. Su trabajo implica una combinaci n
de habilidades t cnicas, conocimiento pr ctico y, en muchos casos, un profundo
entendimiento de los principios matem ticos subyacentes. Este conocimiento se
adquiere a trav s de la experiencia laboral, la transmisi n oral de
conocimientos y, en algunos casos, la formaci n formal en instituciones educativas (Mansilla et al., 2023).
La aplicaci n de la matem tica en el trabajo de
los alba iles es variada y compleja. Desde la planificaci n inicial de un
proyecto hasta la colocaci n de ladrillos y la nivelaci n de superficies, los
alba iles utilizan una amplia gama de conceptos matem ticos en su d a a d a (Uribe & Rojas, 2021). Esto incluye la
geometr a para calcular ngulos y dimensiones, la aritm tica para estimar
cantidades de materiales y costos, y el c lculo para determinar vol menes y
reas
(Nascimento & Linhares, 2019).
Para ilustrar la aplicaci n pr ctica de la
matem tica en el trabajo de los alba iles, consideremos algunos ejemplos
espec ficos. En la construcci n de una pared de ladrillos, por ejemplo, los
alba iles deben calcular el n mero exacto de ladrillos necesarios y
distribuirlos de manera uniforme para garantizar una estructura s lida y
est ticamente agradable. Adem s, al nivelar una superficie, los alba iles
utilizan la geometr a para asegurarse de que la inclinaci n sea uniforme y que
no haya desniveles indeseados.
Si bien es cierto que algunos de los conceptos
matem ticos utilizados por los alba iles pueden ense arse en un aula, gran
parte de este conocimiento se adquiere a trav s de la experiencia laboral y la
pr ctica cotidiana. Los alba iles desarrollan una comprensi n intuitiva de las
matem ticas a medida que enfrentan desaf os y resuelven problemas en el
trabajo, lo que les permite aplicar estos conocimientos de manera efectiva en
situaciones reales.
Aunque el trabajo de los alba iles presenta un
rico campo de estudio para la etnomatem tica, tambi n plantea varios desaf os
metodol gicos (Fern ndez et al., 2021). La naturaleza din mica y fluida del trabajo
de construcci n puede dificultar la observaci n y el registro sistem tico de
las pr cticas matem ticas de los alba iles. Sin embargo, con enfoques
participativos y colaborativos, es posible superar estos desaf os y obtener una
comprensi n m s profunda de la etnomatem tica de los alba iles. Al no valorar la etnomatem tica, se
puede perder la conexi n entre la matem tica acad mica y la vida cotidiana de
las personas. La matem tica est presente en una amplia gama de contextos
culturales y sociales, y no reconocer esta diversidad puede hacer que la
ense anza y el aprendizaje de la matem tica sean menos relevantes y
significativos para los estudiantes.
El objetivo principal de esta investigaci n es
profundizar en la comprensi n de la etnomatem tica desarrollada por los alba iles
en las regiones amaz nicas del Per . Para lograr este objetivo, nos proponemos
identificar y analizar los conceptos matem ticos impl citos en las pr cticas de
los alba iles, as como comprender el papel de la cultura y el entorno natural
en la configuraci n de este conocimiento. Adem s, buscamos destacar la
importancia de reconocer y valorar los conocimientos y pr cticas matem ticas de
las comunidades locales, promoviendo as una mayor inclusi n y apreciaci n de
la diversidad cultural en el campo de las matem ticas.
MATERIALES
Y M TODOS
Tipo de investigaci n
Respecto
al tipo de estudio se considera etnogr fica (Uribe
& Rojas, 2021). Consisti en recabar informaci n, previa
observaci n. Se aplic la t cnica de la encuesta la que, por medio de un
cuestionario, evidenci los procedimientos que realizan los alba iles en la
resoluci n de situaciones matem ticas, empleando las operaciones fundamentales
(suma, resta, multiplicaci n y divisi n) de origen etnomatem tico (Rodr guez, 2021). De la misma forma, se revis
art culos cient ficos referidos al tema con no m s de cinco a os de publicaci n (Gim nez, 2021).
Dise o
del estudio
La
investigaci n se basa en enfoques cualitativos, siendo esta del tipo
descriptivo-etnogr fico (Rodr guez
et al., 2021) y respecto al car cter num rico es cuantitativo dado
que se estudi grupos personas con particularidades culturales, como en el
presente caso los alba iles de la ciudad de Bagua-Amazonas (Barrios et al., 2022).
Poblaci n
y muestra
La
muestra que se utiliz en esta investigaci n mixta es no probabil sticas o
dirigida. Esta elecci n adrede est en funci n de los conocimientos o
particularidades que poseen algunos alba iles que abonan a los prop sitos de
este estudio, raz n por la cual se realizaron (27) entrevistas a alba iles,
dentro de los cuales (02) alba iles de Centro Poblado Tomaque, (03) de la Peca,
(02) de El Parco y (20) alba iles de Bagua capital.
Variables
intervinientes en la investigaci n
Bishop, sostuvo que todas las culturas han
desarrollado conocimientos matem ticos a trav s de seis actividades
principales: contar, ubicar, medir, dise ar, jugar y explicar (Barrios et al., 2022). En base a estos autores
las variables, dimensiones e indicadores en nuestra investigaci n que se evidencia
en la Tabla 1.
T cnicas
o algoritmos realizado por los alba iles en los procesos constructivos
En
la tabla 6, se puede observar un extracto de la entrevista realizada a uno de
los alba iles y dentro de las respuestas se puede evidenciar que el alba il es
consciente que la cantidad de arena que va a requerir para hacer el tarrajeo es
referencial pero que de alguna forma al cliente le dar una idea de cu nto
puede ser su gasto.
Una
de las nociones elementales que evidencia el alba il es el concepto de medir es
decir establecer un elemento patr n para hacer comparaciones que se evidencia
en la figura 4.
El
alba il realiza la operaci n b sica de multiplicaci n para establecer el rea
total a tarrajear e indirectamente realiza una operaci n de multiplicaci n para
establecer un volumen 3 m x 3 m x 2cm llegando a la conclusi n que medio cubo
le va a sobrar pues al cubicar(multiplicar) obtiene 0,18 m3 lo cual
representa menos de la mitad de un cubo.
Seg n
lo vertido por los alba iles, en esta zona nor oriental de Per , los suelos no
son muy compactos (capacidad portante es baja) aunado a ello es una zona muy
calurosa, raz n por la cual los pobladores buscan ciertas caracter sticas en
los materiales de construcci n, existiendo en esta regi n amaz nica diversos
tipos de ladrillos y que, seg n las tiendas de expendio de material de
construcci n, as como la versi n de los alba iles lo cual nos permiti
sistematizar los materiales m s demandados.
Tabla 7. Clasificaci n de
ladrillos para pared utilizados en Bagua capital
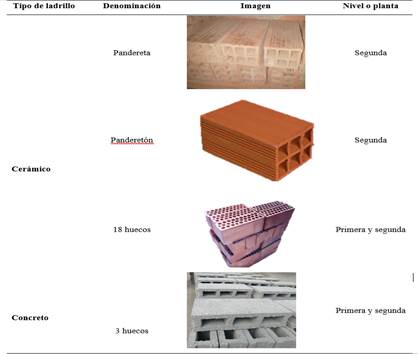
La
etnomatem tica el origen de su aprendizaje En
el intercambio y dialogo realizado con los alba iles de la ciudad de Bagua, concerniente
al origen de su aprendizaje de las operaciones matem ticas como: suma, resta,
multiplicaci n y divisi n utilizadas en su labor. Coinciden que provienen de
sus propias comunidades, del mismo trabajo, que fueron ense adas cuando ellos
eran ayudantes de maestros alba iles. En s ntesis, se podr a sintetizar las
siguientes fuentes:
Al
realizar las labores de ayudante en la construcci n.
Al
ser testigo de c lculos realizados por otros alba iles al ser solicitados por
familiares m s cercanos respecto a trabajos en casa.
Observando
a otros alba iles en actividades de la construcci n.
Conversando
y preguntando a maestros alba iles de m s experiencia.
Cuando
ramos ni os jug bamos a hacer los alba iles
Algunos
casos de evidencia etnomatem tica
Caso: Movimiento
de tierras para cimientos

Figura 5. Dimensiones de zapatas y
movimiento de tierras
El
c lculo del volumen de tierra de una zapata involucra una combinaci n de
m todos tradicionales y modernos, as como una comprensi n pr ctica de los
principios matem ticos subyacentes. La etnomatem tica nos ayuda a apreciar c mo
estos m todos y conocimientos se transmiten y adaptan dentro de diferentes
contextos culturales y comunidades de constructores.
Tabla 8. Sistematizaci n de los
resultados del instrumento aplicado a los alba iles
|
Cliente
|
Pregunta
|
Cu les son las medidas de una zapata
para una casa de dos pisos y cuanta tierra voy a trasladar?
|
|
Alba il
|
Respuesta
|
La medida de una zapata para una casa de
dos pisos la hacemos de 1 m x 1 m 1 m, y como la tierra est comprimida, va
tener que movilizar 1 cubo y medio de tierra.
|
Caso: Uso
de la plomada

Figura 6. Uso de la plomada para
garantizar la verticalidad
El
uso de la plomada en la construcci n est profundamente arraigado en la
etnomatem tica, ya que implica una comprensi n pr ctica de los principios
f sicos y geom tricos para garantizar la precisi n en la alineaci n vertical de
estructuras
Tabla 9. Sistematizaci n de los
resultados del instrumento aplicado a los alba iles
|
Cliente
|
Pregunta
|
C mo me doy cuenta de que una pared esta derecha si no cuento
con un nivel?
|
|
Alba il
|
Respuesta
|
Usamos la plomada, nos sirve para ver si una pared o columna
esta inclinada, la plomada debe separarse unas l neas de la pared, caso
contrario la nivelamos.
|
Caso: Asentar
ladrillos para pared

Figura 7. Proceso para el c lculo
de ladrillos por pared
En
la figura 7, se muestra que los alba iles a menudo emplean patrones espec ficos
al colocar ladrillos para garantizar la estabilidad y la resistencia de la
estructura. Estos patrones pueden variar seg n la tradici n local y la
experiencia transmitida de generaci n en generaci n.
Tabla 10. Sistematizaci n de los
resultados del instrumento aplicado a los alba iles
|
Cliente
|
Pregunta
|
C mo sabe cu l la distancia de separaci n entre los ladrillos
al momento de asentarlos?
|
|
Alba il
|
Respuesta
|
El objetivo es que los ladrillos amarren sin perder estabilidad,
depende del tama o la separaci n puede ser entre 2 a 5 cent metros
aproximadamente y cuando los asiento, solo los separo y queda parejo.
|
Caso: Tarrajeo
de pared

Figura 8. Proceso para nivelar la
pared durante el tarrajeo
En
la figura 8 se refleja que, aunque el tarrajeo de una pared puede parecer un
proceso puramente pr ctico, est impregnado de aspectos matem ticos que
reflejan la cultura y la tradici n de quienes lo realizan. La etnomatem tica
nos ayuda a reconocer y apreciar estos aspectos en contextos cotidianos.
Tabla 11. Sistematizaci n de los
resultados del instrumento aplicado a los alba iles
|
Cliente
|
Pregunta
|
C mo logra nivelar la pared durante el tarrajeo?
|
|
Alba il
|
Respuesta
|
Antes de empezar a tarrajear, coloco puntos a veces 4, los fijo
con diablo fuerte (mezcla de cemento y yeso), estos puntos me permiten
guiarme y con ayuda de una regla de aluminio voy barriendo la mezcla hasta
finalmente pulir con una plancha y queda bien lisa.
|
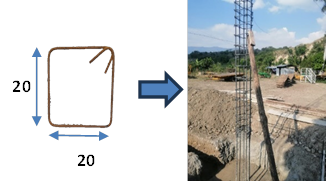
Caso: Armaz n
de acero para columnas y vigas

Figura 9. Proceso para el
enfierrado de columnas y vigas
La
figura 9, evidencia las pr cticas matem ticas de diferentes culturas y
comunidades. En el contexto de la construcci n civil, la etnomatem tica podr a
explorar c mo ciertas comunidades utilizan el conocimiento matem tico en la
planificaci n y ejecuci n de proyectos de construcci n, incluyendo el c lculo
de dimensiones y espaciamientos del acero utilizado, como se observa en las
respuestas de la tabla 12.
Tabla 12. Sistematizaci n de los
resultados del instrumento aplicado a los alba iles
|
Cliente
|
Pregunta
|
C mo sabe la distancia entre los estribos para una columna?
|
|
Alba il
|
Respuesta
|
Cerca de la base o la zapata, los estribos deben estar m s
juntos, lo hacemos dejando 5 cent metros en la zapata, m s arriba es cada 10
cm y ya los restantes cada 20 cm eso aprend y hasta ahora lo hago.
|
DISCUSI N
Integraci n
de conceptos matem ticos y pr ctica laboral
Uno
de los hallazgos clave de esta investigaci n es la integraci n de conceptos
matem ticos en la pr ctica laboral de los alba iles. Se observa c mo estos
trabajadores utilizan una amplia gama de conceptos, desde la geometr a hasta el
c lculo, en la planificaci n y ejecuci n de sus tareas diarias. Esta
integraci n demuestra que las matem ticas no son un concepto abstracto separado
de la vida cotidiana, sino una herramienta pr ctica y tangible que se utiliza
de manera efectiva para resolver problemas concretos(Fuentes,
2019).
Conocimiento
adquirido a trav s de la experiencia y la tradici n oral
Otro
hallazgo importante es el papel central que juega la experiencia y la tradici n
oral en la adquisici n y transmisi n del conocimiento matem tico entre los
alba iles. Aunque algunos conceptos matem ticos pueden ense arse en un aula,
gran parte de este conocimiento se adquiere a trav s de la pr ctica laboral y
la interacci n con colegas m s experimentados. Esta observaci n destaca la importancia
de reconocer y valorar las formas de conocimiento no formal en el mbito de la
etnomatem tica(S nchez, 2019).
Adaptaci n
de conceptos matem ticos al contexto cultural y ambiental
Un
aspecto interesante de la etnomatem tica de los alba iles es c mo adaptan y
aplican conceptos matem ticos al contexto cultural y ambiental de las regiones
amaz nicas del Per . Por ejemplo, se observa c mo los alba iles utilizan la
geometr a para trabajar con materiales naturales como la madera y el barro, as
como para dise ar estructuras que sean resistentes a las condiciones clim ticas
extremas de la selva. Esta adaptaci n demuestra la flexibilidad y la
creatividad del pensamiento matem tico de los alba iles, as como su profunda
comprensi n del entorno en el que operan(Pereira & Batallas, 2019).
Desaf os
y oportunidades en la investigaci n de la etnomatem tica de los alba iles
Si
bien esta investigaci n ha proporcionado una visi n valiosa de la
etnomatem tica de los alba iles en las regiones amaz nicas del Per , tambi n ha
identificado varios desaf os y oportunidades para futuras investigaciones en
este campo. Por ejemplo, la naturaleza din mica y fluida del trabajo de
construcci n puede dificultar la observaci n y el registro sistem tico de las
pr cticas matem ticas de los alba iles. Sin embargo, con enfoques
participativos y colaborativos, es posible superar estos desaf os y obtener una
comprensi n m s profunda de la etnomatem tica de los alba iles (Rodr guez & Saiz,
2022).
Precisi n
en el c lculo de materiales y optimizaci n de recursos
Uno
de los resultados m s destacados es la precisi n con la que los alba iles
calculan la cantidad de materiales necesarios para un proyecto de construcci n.
A trav s de m todos pr cticos y t cnicas transmitidas de generaci n en
generaci n, los alba iles desarrollan habilidades para estimar con precisi n la
cantidad de ladrillos, cemento, arena, y otros materiales requeridos para
completar una tarea espec fica(Pereira & Batallas, 2019). Este resultado
demuestra la eficacia del conocimiento matem tico informal que los alba iles
aplican en su trabajo diario. Los alba iles suelen adaptar sus m todos de
c lculo a las condiciones espec ficas del sitio de construcci n y a las
necesidades del proyecto en cuesti n. Esta capacidad de adaptaci n resalta la
flexibilidad del conocimiento matem tico de los alba iles, quienes pueden
ajustar sus c lculos seg n diferentes variables, como el tama o de la
estructura, la calidad de los materiales disponibles y las condiciones
clim ticas(Leyton, 2019). Los alba iles son
expertos en optimizar el uso de recursos, calculando cuidadosamente la cantidad
justa de materiales necesarios para evitar desperdicios y minimizar costos.
Esta habilidad para maximizar la eficiencia en el uso de materiales es
fundamental para el xito de un proyecto de construcci n y demuestra la
aplicaci n pr ctica del conocimiento matem tico en la gesti n de recursos(Concha et al., 2021).
CONCLUSIONES
La etnomatem tica reconoce y valora las
diversas formas en que diferentes culturas y comunidades aplican y desarrollan
el pensamiento matem tico en su vida cotidiana. Al poner en valor la
etnomatem tica, se promueve una mayor apreciaci n de la diversidad cultural y
se brinda a los pobladores en general la oportunidad de aprender sobre las
contribuciones matem ticas de diferentes grupos tnicos y culturales en todo el
mundo.
La observaci n de los alba iles en su entorno
laboral confirma que poseen un conjunto de conocimientos matem ticos informales
que han adquirido a trav s de la experiencia pr ctica y la transmisi n
intergeneracional. Esta validaci n reconoce la importancia y el valor de los
conocimientos no formales en la resoluci n de problemas pr cticos en el campo
de la construcci n.
Los alba iles demuestran una capacidad notable
para aplicar conceptos matem ticos de manera creativa y flexible para resolver
una variedad de problemas en la construcci n de edificaciones. Esta habilidad
refleja una comprensi n profunda de los principios matem ticos subyacentes y su
capacidad para adaptarse a diferentes situaciones y desaf os en el lugar de
trabajo.
REFERENCIAS
BIBLIOGR FICAS
Alsina, . (2019).
Conexiones matem ticas a trav s de actividades STEAM en Educaci n Infantil. Revista
Iberoamericana de Educaci n Matem tica, 1(58), 168 191.
https://dugi-doc.udg.edu/handle/10256/18073
Aroca, A. (2022). Un
enfoque did ctico del programa de etnomatem ticas. Revista TED, 2(52),
211 248. https://doi.org/10.17227/ted.num52-13743
Barrios, M., Sarmiento,
J., Rodr guez, C., & Lafaurie, J. (2022). An lisis de las conexiones
etnomatem ticas en la elaboraci n y comercializaci n de arroz chino en el sur
del departamento del Atl ntico, Colombia. Revemop, 4(1), 1 26.
https://doi.org/10.33532/revemop.e202221
Concha, R., San Mart n,
N., & Friz, M. (2021). La etnomatem tica en el proceso de comunicaci n y
construcci n de saberes: Una aproximaci n entre la matem tica y la ling stica
de las comunidades. Revista Aportes, 1(31), 23 32.
http://www.scielo.org.bo/scielo.php?script=sci_arttext&pid=S2306-86712021000200003
Estela, R., Contreras,
E., V squez, J., P sito, D., V squez, J., & Ugkum, S. (2021).
Etnomatem tica: Hidr ulica l dica a partir de las figuras geom tricas de la
cer mica awaj n. Revista de Investigaci n Cient fica DEKAMU AGROPEC, 2(2),
62 74. https://doi.org/10.55996/dekamuagropec.v2i2.61
Fern ndez, A., Blanco,
H., & Oliveras, M. (2021). Aplicaci n de un instrumento para valorar la
idoneidad did ctica etnomatem tica a una propuesta de ense anza- aprendizaje
sobre patrones de medida no convencionales. Revista Bolema - Mathematics
Education Bulletin, 35(71), 1845 1875.
https://doi.org/10.1590/1980-4415V35N71A28
Fuentes, C. (2019).
Articulaci n de la etnomatem tica y las propuestas decoloniales: Una invitaci n
a la re-existencia. Revista Latinoamericana de Etnomatem tica, 12(3),
59 82. https://www.redalyc.org/articulo.oa?id=274063987005
Gim nez, A. (2021). La
tarea de levantar paredes con ladrillo: Un an lisis desde la teor a
antropol gica de lo did ctico. Revista Cient fica EFI-DGES, 7(12),
49 64. http://ppct.caicyt.gov.ar/index.php/efiEDUCACI N,FORMACI NEINVESTIGACI N
Leyton, E. C. (2019). Una
mirada a la Etnomatem tica. Autocton a. Revista de Ciencias Sociales e
Historia, III(2), 244 267. https://doi.org/10.23854/autoc.v3i2.119
Mansilla, E., Z iga, .,
Vel squez, F., Montecinos, M., Castro, A., & Rodr guez, C. (2023).
Exploraci n etnomatem tica en los procesos de restauraci n de iglesias
patrimoniales de Chilo -Chile. Revista de Investigaci n, Desarrollo e
Innovaci n, 13(2), 299 314.
https://doi.org/10.19053/20278306.v13.n2.2023.16836
Morales, L., &
Rodr guez, C. (2022). Medidas no convencionales en libros de texto mexicanos.
Un an lisis desde la Etnomatem tica y el Enfoque ontosemi tico. Journal of
Research in Mathematics Education, 11(1), 33 70. https://doi.org/10.17583/redimat.8646
Nascimento, S., &
Linhares, J. (2019). Etnomatem ticas y pr ctica docente ind gena: la cultura
como eje integrador. Revista Cient fica Hiapt a, 4(1), 102 115.
https://ojs.ifsp.edu.br/index.php/hipatia/article/view/1092
Pereira, L. (2019). El
universo simb lico de los astros como aspecto etnomatem tico. Revista
Latinoamericana de Etnomatem tica, 12(2), 82 102.
https://www.redalyc.org/journal/2740/274063607004/html/
Pereira, L., &
Batallas, B. (2019). Hacia una perspectiva etnomatem tica del quipu incaico
como puente entre el sistema contable y la escritura. Revista
Latinoamericana de Etnomatem tica, 12(2), 62 81.
https://revista.etnomatematica.org/index.php/revlatem/article/view/503
Rodr guez, A., &
Saiz, M. (2022). Etnomatem ticas para el fortalecimiento de operaciones b sicas
en ni os ind genas piapocos. Revista Rastros y Rostros Del Saber, 7(13),
7 30.
Rodr guez, C. (2021).
Conexiones etnomatem ticas entre conceptos geom tricos en la elaboraci n de las
tortillas de Chilpancingo, M xico. Revista de Investigaci n, Desarrollo e
Innovaci n, 11(2), 273 296. https://doi.org/10.19053/20278306.v11.n2.2021.12756
S nchez, Y. (2019).
Complejidad-cotidianidad-etnomatem tica en la ense anza de las matem ticas. Revista
PRAXIS INVESTIGATIVA REDIE, 11(20), 23 36.
https://dialnet.unirioja.es/servlet/articulo?codigo=6951587
Uribe, D., & Rojas, O. (2021). Patrones de
medici n (Jaaniapala ayaawata) en pr cticas culturales de la Naci n Way u de la
Guajira colombiana. Revista Latinoamericana de Etnomatem tica, 14(2),
76 96. https://doi.org/10.22267/relatem.21142.8
![]() , Elisa Contreras Barsallo[2]
, Elisa Contreras Barsallo[2]![]() ,
Alcides Ra l Cuti Gutierrez[3]
,
Alcides Ra l Cuti Gutierrez[3]![]()
![]() , Carlos
Carcausto Quispe4
, Carlos
Carcausto Quispe4![]() , Giovanna
Guzm n C ceres[5]
, Giovanna
Guzm n C ceres[5]![]()
![]() , Edinson
Figueroa Fern ndez1
, Edinson
Figueroa Fern ndez1![]() ,
Luis Miguel Villegas Santamar a[6]
,
Luis Miguel Villegas Santamar a[6]![]()